Structure of a System

We’ve already seen what a system is—a whole made up of interdependent parts. Now we move a step further to understand its internal architecture, or what we call its structure.

Just like the framework of a building tells us how the rooms, doors, and walls are connected, the structure of a system tells us:

• What components the system has,
• How they’re linked to each other,
• And how the system connects with the outside world.

🧠 Three Fundamental Components of Any System

As per systems theory, a system consists of three key parts:

Component	Description
1. A Set of Elements	The basic units or entities inside the system
2. A Set of Links	The relationships or interactions between elements
3. Links with the Environment	Interactions between the system and things outside it

Let’s understand each in detail.

🔹 Elements: The Building Blocks

Think of elements as the smallest units that make up a system.

• In a city, elements might be houses, roads, people, or institutions.
• In a river system, elements could be tributaries, sediments, riverbanks, etc.

From a mathematical point of view, elements are primitive terms—just like a point in geometry. We don’t define them further; we just accept them as the basic components.

📌 Important Point: The elements you identify depend entirely on the scale at which you’re observing the system.

Let’s take some examples:

System	Elements (at different scales)
World Economy	Countries
A Country’s Economy	Firms and Organizations
An organization	Departments
A Department	People
A Person	Organs or Cells
Traffic System	Cars (each car is an element, but also a system!)

So, you see, a car might be an element in a traffic system, but it’s also a system in itself—with engine, gears, electronics, etc.

This means:

🔁 An element can be both a part and a whole, depending on how broadly or narrowly you’re looking.

🔄 Links: The Relationships Between Elements

We’ll discuss this in more detail in the next part, but in brief:

• These are the connections or flows—of matter, energy, information—that happen between elements within the system.

For example:

• In a climate system, the link between temperature and precipitation could be through evaporation.
• In a settlement system, links might be roads, trade routes, or communication networks.

These links define the structure, because a system isn’t just about what is inside, but also how those things are connected.

🌐 Links with the Environment

A system doesn’t exist in isolation.

There are always inputs coming from the environment and outputs going out.

Examples:

• A river system receives rainfall (input) and sends out discharge into the ocean (output).
• A firm receives raw materials and sends out products.

These external links help us classify systems as open or closed, which we’ll cover in the next topic.

📉 Function and Development of a System

• Structure is about what the system contains and how it’s arranged.
• Function is about what the system does—it’s the flow or exchange that happens along the links.
• Development is about how both structure and function change over time.

Imagine a city:

• Structure: Roads, neighbourhoods, offices.
• Function: Traffic movement, economic activity.
• Development: Urban sprawl, infrastructure upgrade, gentrification.

📏 Scale Determines the Element

One of the most fascinating parts of this discussion is the idea that:

❗ The definition of an element depends on the scale at which you observe the system.

Let’s reinforce this with an example:

• At a global scale, a country is an element in the international system.
• At the national scale, that same country contains firms.
• And so on—down to the level of individual human beings, or even biological cells.

This nested, hierarchical view is very common in geography and helps us build multi-scalar models.

🧮 Mathematical Systems Theory Viewpoint

In mathematical terms: An element is a variable, not an object.

This means we don’t treat the object (e.g., a farm) as the element—we treat its attributes (e.g., size, crop type, yield) as variables.

That’s a subtle but powerful shift:

• We’re analysing characteristics, not just things.
• This makes system analysis quantifiable and logical.

🔁 Diagrams: Blalock & Blalock’s Two Views of Interaction

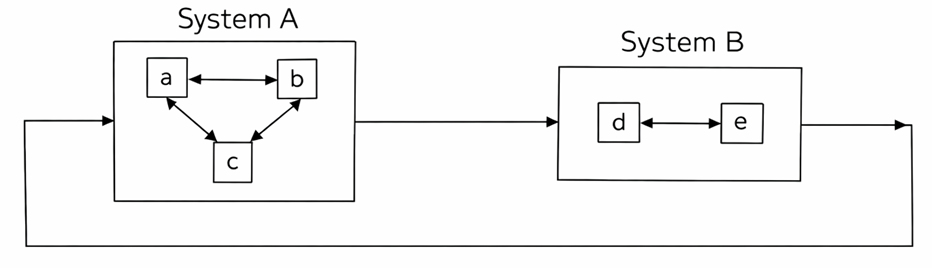
Above Diagram: Shows System A and System B interacting as whole units, while internal interactions happen within each system.

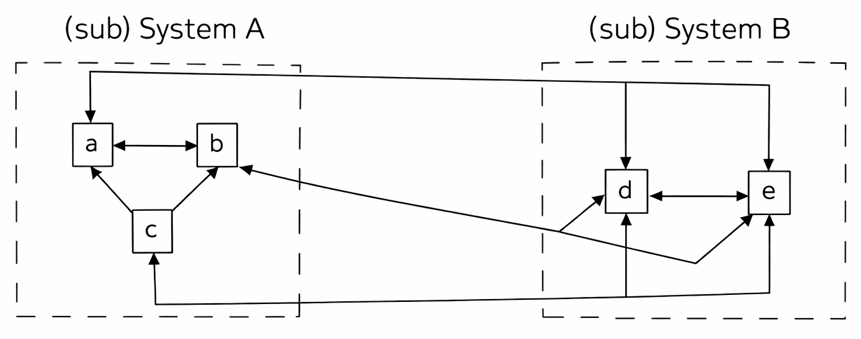
Zooms in to show interactions between smaller parts of System A and B.

This visualizes how systems interact both as wholes and through their sub-parts.

🔗 What Are Links in a System?

• In any system, elements alone don’t define it—what really gives it life are the relationships or interactions between these elements.
• These are called links, and they define how one element affects another.

📌 Think of elements as nodes in a network, and links as the arrows or paths that connect them.

🧩 Three Basic Forms of Relationships

1️⃣ Series Relation

🧠 “A leads to B” — Classic cause-and-effect.

• Definition: A unidirectional and irreversible link between elements.
• Symbolically, a_i → a_j.
• This is the simplest form and represents the linear logic that traditional science often uses.

Example (India):

• Productivity of rice in Punjab → depends on availability of irrigation.
• Cultivation of saffron in Kashmir → depends on Karewa soil.

📝 Key Characteristics:

• Sequential.
• Easy to understand and model.
• Good for simple cause-effect chains.

🖼️ Diagram:

• One box leads to the next → a_i → a_j → a_k.

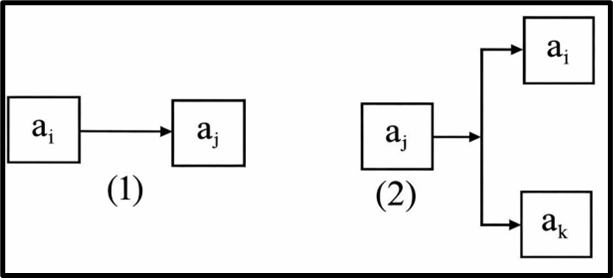
2️⃣ Parallel Relation

🧠 “Many elements affect one, or one element affects many.”

• Definition: Occurs when multiple elements influence a single element, or vice versa.
• It’s a more complex interaction compared to series relations.

Example:

• Precipitation and temperature → both influence vegetation.
• Vegetation in turn affects rainfall patterns and temperature conditions (this part can begin to introduce feedback, too).

📝 Key Characteristics:

• Allows for multiple causes or multiple effects.
• More realistic in environmental and social systems.

🖼️ Diagram:

• Arrows from a_i and a_k both pointing to a_j.
• Or a_j branching out to multiple other elements.

3️⃣ Feedback Relation

🔁 “An element affects itself—directly or indirectly.”

• Definition: A relationship where the output of a system feeds back as an input to the same element.
• This is dynamic and introduces the self-regulating or self-reinforcing nature of systems.

Example:

• Leguminous crops (like beans or peas) enrich the nitrogen in the soil.
• Improved nitrogen levels → enhance their own productivity in the next cycle.

📝 Key Characteristics:

• Introduces loops.
• Can be positive feedback (amplifies change) or negative feedback (stabilizes system).
• Crucial in climate systems, economic systems, ecosystems, etc.

🖼️ Diagram:

• A looped arrow returning to the same element, or a cycle of arrows forming a closed circuit.

🔍 Summary

Figure	Relationship Type	Visual Clue	Description
1	Series	ai → aj → ak	Linear, one-way influence
2	Parallel	aj → ai & ak	Many-to-one or one-to-many
3	Feedback	ai → aj → ai	Circular loop, self-influence
4	Simple Compound Relation	Mix of series + parallel	Moderate complexity
5	Complex Compound Relation	Web of interactions	High complexity, real-world-like systems

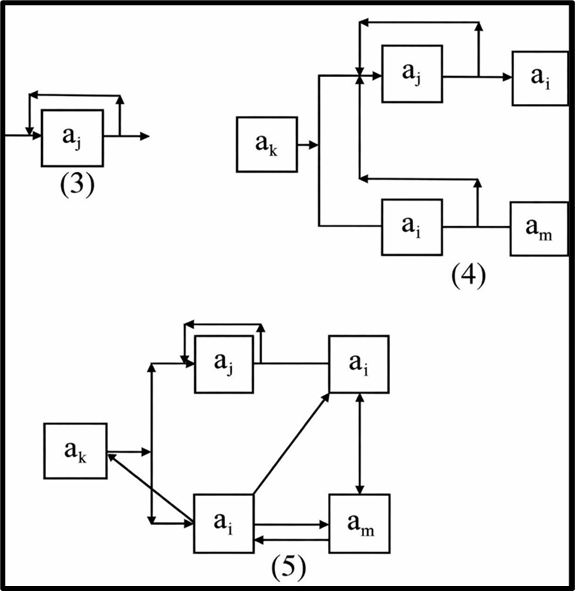
🧠 Why Is This Important in Geography?

• Helps model natural systems like climate, hydrology, ecosystems.
• Applies to human systems: urban planning, population dynamics, economic zones.
• Teaches us how complexity emerges from simple relationships.